|
|
|
It was Albert Einstein who first realized this must be the way nature works. Though in popular thought Einstein's "E=MC^2" tops the charts, he won the Nobel prize for his clever take on a formula first proposed by physicist Max Planck: E=h * frequency. "E" stands for energy and "h" is just a conversion factor similar to the conversion factor we use when we change Dollars to Euros. In the case of light, "h" converts frequency to energy.
| As an example, let's calculate the energies of a safe green photon and a dangerous UV photon.
Safe green photon (550 nanometer wavelength): Frequency = 5.45e+14 cycles per second (frequency is obtained by dividing the speed of light by the wavelength) h = 6.63e-34 joule-second Energy = h * frequency = 3.61e-19 joules Dangerous UV photon (275 nanometer wavelength): Frequency = 1.09e+15 cycles per second h = 6.63e-34 joule-second Energy = h * frequency = 7.23e-19 joules |
What if we asked for a UV photon of the same frequency but with less energy? The answer is: there's no such thing! This answer would have surprised physicists before Einstein who believed that light was a wave. In the wave theory you can reduce the energy of a light wave as much as you want by lowering the amplitude (height) of the wave, whereas in the particle theory, the energy of a single photon—given by E=h * frequency—is the minimum amount of energy that a light beam of that frequency can have. Moreover, you can only increase the beam energy by adding another photon, so the beam energy can only increase in steps. Einstein's interpretation of the equation "E = h * frequency" played a major part in the revolution in physics that we now call quantum theory. The first physicist to state the famous formula, Max Planck, discovered that a model which treats light as though it came in discrete bundles of energy agreed with experimental observations that the wave theory of light couldn't explain. Einstein's view was that there is no "as though" about it, the equation is telling it as it is, and light actually does come in bundles whose energy is given by E= h * frequency. Same equation, different ways of seeing what it means.
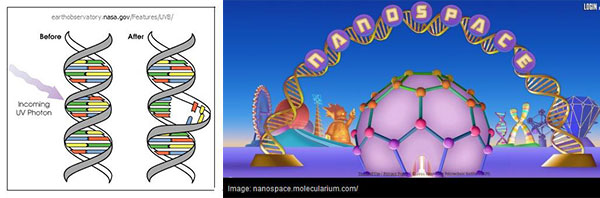
It's a fair question to ask why we still use terms like "wavelength" if we now know that light is a particle. This isn't just a historical leftover or a matter of hard-to-discard tradition. Quantum theory involves probability calculations with wavelike expressions as an essential feature. But the wavelike nature is a characteristic of the quantum probabilities not of the photon per se. Because when it comes to interacting with matter—say, a high energy UV photon interacting with a strand of DNA—light acts like a particle not a wave: the molecular bond is immediately broken as though it got hit by tiny rock.

|
Health science is among the numerous applications benefiting from the particle theory of light. For example we already mentioned that a green photon at 550 nanometer wavelength is eye-safe whereas a UV photon at 275 nanometers is not, but what about photons with in-between energies? Can they interfere with the normal chemistry of the eye? The 400-500 nanometer wavelength range (violet to blue) is known as high-energy visible (HEV) light, and some experts have eye health concerns regarding this part of the visible spectrum. Exposure to high intensity light in this wavelength range has caused eye damage in laboratory animals, suggesting the possibility that long term exposure to lower levels of HEV could be harmful to human eyes. If so, the explanation of the causes will depend on the imagined "You Must Have This Amount of Energy to Break this Bond" sign on the biological molecules involved.
 |